万博体育app

在固体物理中，材料的振动态密度与电子能谱长期以来是核心研究对象，因为它们能够被实验直接测量并与宏观物性建立联系。然而，量子材料研究的发展表明，仅关注本征值（能量谱）并不足以完整理解体系行为：本征态（波函数/本征矢量）的几何与相位结构包含关于量子态干涉与叠加的关键信息，这一视角推动了拓扑物态、量子霍尔效应等复杂物理现象的几何化理解。我们注意到，类似的研究范式正在逐步延伸至玻璃物理：相较于对振动态密度的广泛研究，直接针对振动本征模空间结构、尤其是其拓扑特征的系统工作仍然较少。最近，研究人员在二维体系中证明，低频本征矢量中的拓扑缺陷几何与非晶塑性响应之间存在紧密联系（Nat. Commun. 2023, 14:2955），并随后在二维胶体玻璃实验中得到检验（Nat. Commun. 2025, 16:55）。在此基础上，本次研究进展将这一拓扑视角推广至更贴近真实材料的三维玻璃体系，旨在回答：三维中拓扑缺陷如何组织？其几何统计规律是什么？以及它们与塑性行为之间是否存在可定量的内在联系？

我们采用经典 Kob-Andersen 二元 Lennard-Jones 玻璃模型，进行大尺度分子动力学模拟（体系规模 80 万粒子）与计算分析。样品在T=0.43（略低于模式耦合理论预测的玻璃化温度附近）充分平衡后缓慢冷却至零温。随后对 Hessian（动力学矩阵）进行对角化，获得最低频的10, 000个振动本征模式。为在三维中识别本征矢量场的拓扑缺陷，我们将离散粒子本征矢量通过高斯加权插值构造成连续矢量场，并投影到叠加的规则立方网格上。对于每个体素单元的六个面，计算相位沿边界的绕数：若相位变化为，则该面被涡旋/反涡旋穿过；相位变化为零则表示无奇点。通过追踪相邻单元中奇点信息的连通性，可以在三维空间中描绘拓扑缺陷的几何形貌。在力学响应方面，我们对零温玻璃施加准静态剪切变形，并采用非仿射位移指标识别塑性事件的空间位置与参与粒子集合。由此我们能够在同一体系中对比：低频本征模拓扑缺陷的几何结构与剪切诱发塑性事件的空间组织之间的关系。

主要研究结果：

（1）缺陷数量的频率标度： 研究发现，在低频 Debye 区域（频率小于约1.0）内，拓扑缺陷的数量与成正比，这一规律与我们此前在二维体系中的结论一致。结合本征矢量场的几何性质，我们认为该标度来源于低频模式的声学特征：低频本征模主要是横声学波的叠加，在三维中形成准一维的拓扑涡旋线结构，其特征间距由波长控制（～ω⁻¹），从而自然导出的缺陷密度标度。

（2）缺陷空间组织的尺度不变性： 通过定义缺陷-缺陷的空间关联函数，我们发现同号缺陷的关联在较大尺度区间内呈幂律衰减，指数约为-5/3，对应分形维数4/3。该结果表明在三维玻璃中，低频拓扑缺陷以具有尺度不变统计特征的细丝状结构组织。随着频率升高，幂律区间逐渐缩短，可定义出频率依赖的特征长度。在低频区（）我们进一步观察到与呈线性关系，其比例系数对应声速，从而为“低频缺陷结构与声学模式”之间的关联提供了额外证据。

（3）与塑性事件的定量对应： 准静态剪切下，我们识别到塑性事件位置在空间上具有稳定且可重复的组织特征；尤其是其两点关联函数同样表现出指数约为-5/3的幂律衰减，并与拓扑缺陷网络的关联行为一致。这提示塑性事件的空间形态并非随机，而是与低频本征模所“预设”的拓扑几何结构存在内禀对应关系。进一步的统计表明，在一定频率区间内（），塑性事件与带负拓扑电荷的缺陷段（对应局域鞍点型结构）呈显著相关，且在附近达到峰值。这一结果与二维体系中“负缺陷更能标记塑性热点”的结论相一致，在小应变（）时，塑性事件发生在负拓扑缺陷附近的概率是均匀分布预期值的两倍左右。

综上所述，本项研究工作把“位错—塑性”的经典晶体图像，推广到无长程序的非晶固体。我们建立了三维玻璃中“本征模拓扑缺陷几何—塑性耗散结构”之间的定量联系。在晶体中，位错线是塑性形变的主要载体，其几何与动力学受晶格对称性严格约束；而在玻璃中，低频声学模式与无序结构的耦合叠加生成了更复杂的拓扑涡旋线网络，这些线状结构为理解塑性活动的空间组织提供了新的几何框架。我们的结果也提示，玻璃中的塑性行为不能仅作为局域事件在Eshelby场中相互作用来理解，而需要将由本征模几何结构与长程弹性相互作用共同导致的非局域关联纳入考虑，这为解释玻璃断裂中的显著有限尺寸效应提供了自然线索。值得注意的是，本研究发现的拓扑涡旋线的排布特征与量子流体/气体中涡旋线的拓扑奇点具有相似性，后者与能量级联和耗散过程密切相关，表现出标度不变行为。这种标度不变性暗示了在广泛的物理体系中缺陷组织和相互作用可能存在普适性规律，为建立跨越晶体、非晶和多晶材料的能量耗散过程统一描述框架提供了微观理论基础。

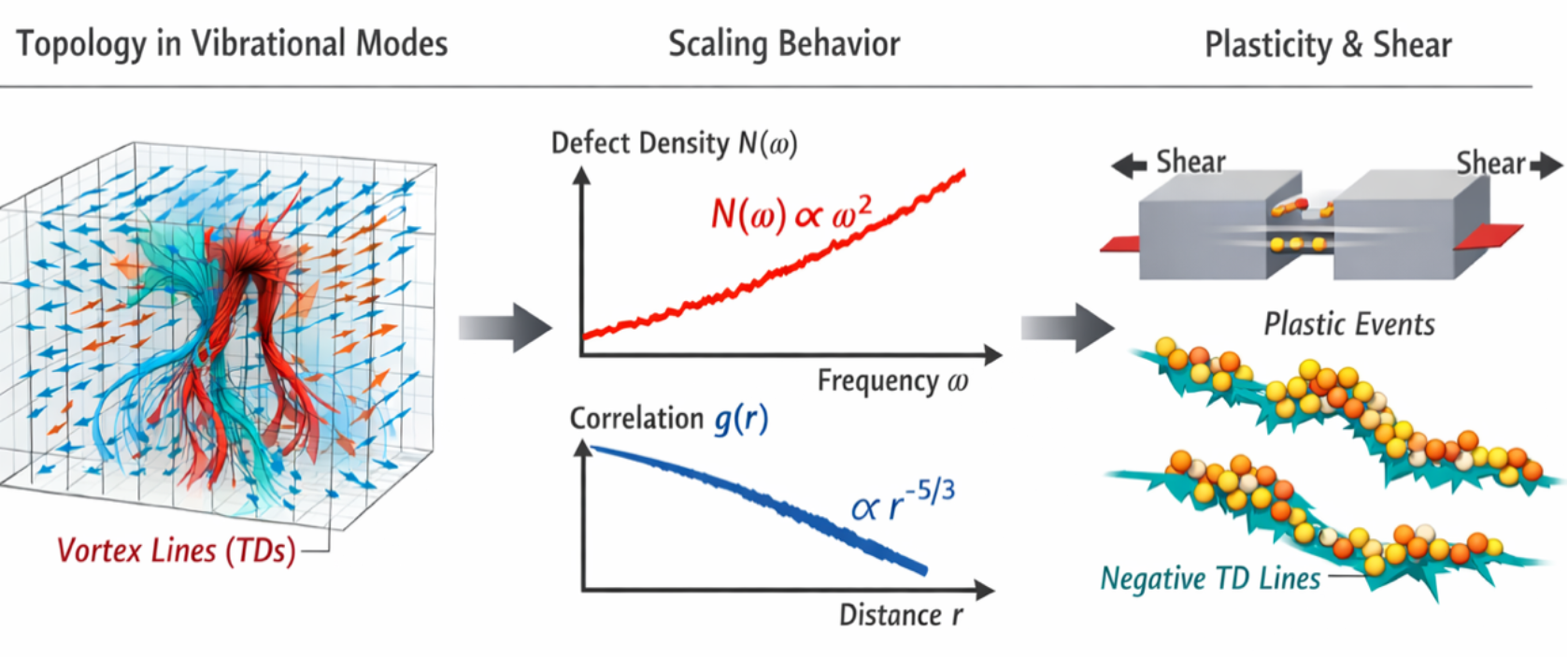
Graphical abstract：从“只看振动态密度”转向“看本征模本身的几何与拓扑”，并通过相位绕数识别三维中的拓扑缺陷，这些缺陷并非零散“点”，而是准一维的涡旋线，在空间中形成特定几何结构。玻璃的塑性重排并非局部随机，而是被低频本征模的拓扑几何所“预编程”。（图片借助生成式人工智能制作产生）

该工作由武振伟副教授与法国CNRS/UGA物理交叉科学实验室Jean-Louis Barrat教授、和蒙彼利埃大学Walter Kob教授合作完成。该研究得到了国家自然科学基金面上、重点、和青年项目（Grant Nos：12474184, 52031016, 11804027），以及国家留学基金的资助。

文章链接（DOI）：//doi.org/10.1038/s41467-025-66923-1

供稿：武振伟

编辑：郝林青

审核：李   辉